Posts

拉格朗日函数

MATH

Python 代码

拉格朗日函数

原问题

假设有一个在限定条件下需要求极值的问题，如下：

min⁡xf(x),x∈Rns.t. gi(x)≤0,i=1,2,…,mhi(x)=0,i=1,2…,q\min_x f(x),x\in\mathbb{R}^n\\ s.t.\ g_i(x)\le0,i=1,2,\dots,m\\ h_i(x)=0,i=1,2\dots,q

拉格朗日函数

L(x,λ,μ)=f(x)+∑λigi(x)+∑μihi(x)L(x,\lambda,\mu)=f(x)+\sum\lambda_i g_i(x)+\sum \mu_i h_i(x)

转化为原问题的等价形式

min⁡xmax⁡λ,μL(x,λ,μ)s.t. λ≥0\min_{x}\max_{\lambda,\mu} L(x,\lambda,\mu)\\ s.t.\ \lambda\ge0

理解为什么原问题的拉格朗日函数形式等价于原问题？

xx 在 LL 中是可以取全域的（没有限制条件了，可以随便瞎取），LL 只限制了 λ\lambda.

先考虑 max⁡λ,μL(x,λ,μ)\max_{\lambda,\mu} L(x,\lambda,\mu)

x不在可行域内→max⁡λ,μL(x,λ,μ)=f(x)+∞+∞=∞x在可行域内→max⁡λ,μL(x,λ,μ)=f(x)+0+0=f(x)↓min⁡xmax⁡λ,μL(x,λ,μ)=min⁡x{f(x),∞}=min⁡xf(x)x 不在可行域内\rightarrow \max_{\lambda,\mu} L(x,\lambda,\mu)=f(x)+\infty+\infty=\infty\\x 在可行域内\rightarrow \max_{\lambda,\mu}L(x,\lambda,\mu)=f(x)+0+0=f(x) \\ \downarrow\\ \min_x\max_{\lambda,\mu} L(x,\lambda,\mu)=\min_x\{f(x),\infty\}=\min_{x}f (x)

理解什么是互补松弛？

z

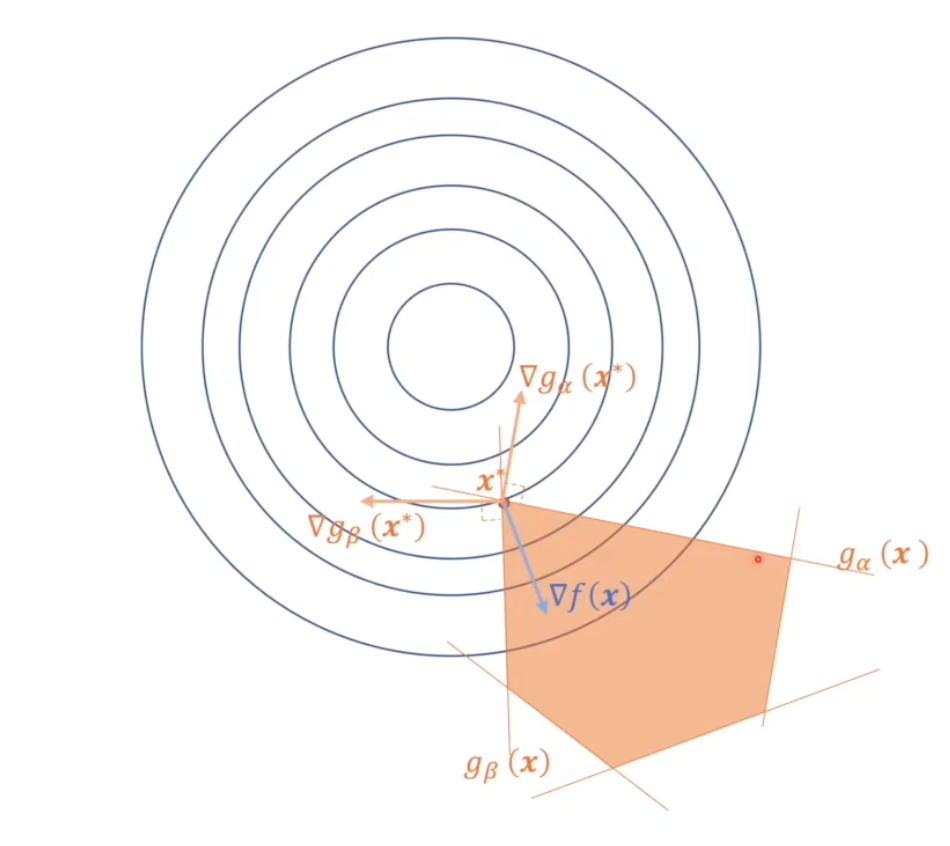
假设有五个不等式约束函数 gi(x)g_i(x)，只有其中两个约束 gαg_{\alpha} 和 gβg_{\beta} 在求极值的时候用上了。因此其他约束函数的系数 λi=0\lambda_i=0，λα,λβ≥0\lambda_{\alpha},\lambda_{\beta}\ge0. 通俗理解就是，约束函数用上了（紧致），则系数不等于 0（松弛），约束函数没用上（松弛），则系数等于 0（紧致）.

互补松弛定理 One of KKT conditions

所有 λi≥0{λi=0,gi(x) 松弛λi>0,gi(x) 紧致\lambda_i \ge0 \begin{cases}\lambda_i=0, g_i(x)\ 松弛\\ \lambda_i\gt0,g_i(x)\ 紧致\end{cases}

对偶函数

假设 g(λ,μ)=min⁡xL(x,λ,μ)g(\lambda,\mu)=\min_{x} L(x,\lambda,\mu)，这个也被称为原问题的对偶函数

max⁡λ,μg(λ,μ)→max⁡λ,μmin⁡xL(x,λ,μ)s.t. λ≥0↓max⁡λ,μg(λ,μ)s.t. ∇xL(x,λ,μ)=0λ≥0\max_{\lambda,\mu} g(\lambda,\mu)\rightarrow \max_{\lambda,\mu}\min_{x} L(x,\lambda,\mu)\\ s.t.\ \lambda\ge0\\ \downarrow\\ \max_{\lambda,\mu} g(\lambda,\mu)\\ s.t.\ \nabla_x L(x,\lambda,\mu)=0\\ \lambda\ge0

理解什么是对偶问题？

对偶问题的特性：无论原问题是什么，换成对偶问题后都是一个凸问题

凸集 CC 的定义：∀x1,x2∈C,0≤θ≤1→θx1+(1−θ)x2∈C\forall x_1,x_2\in C,0\le\theta\le1 \rightarrow \theta x_1+(1-\theta)x_2 \in C

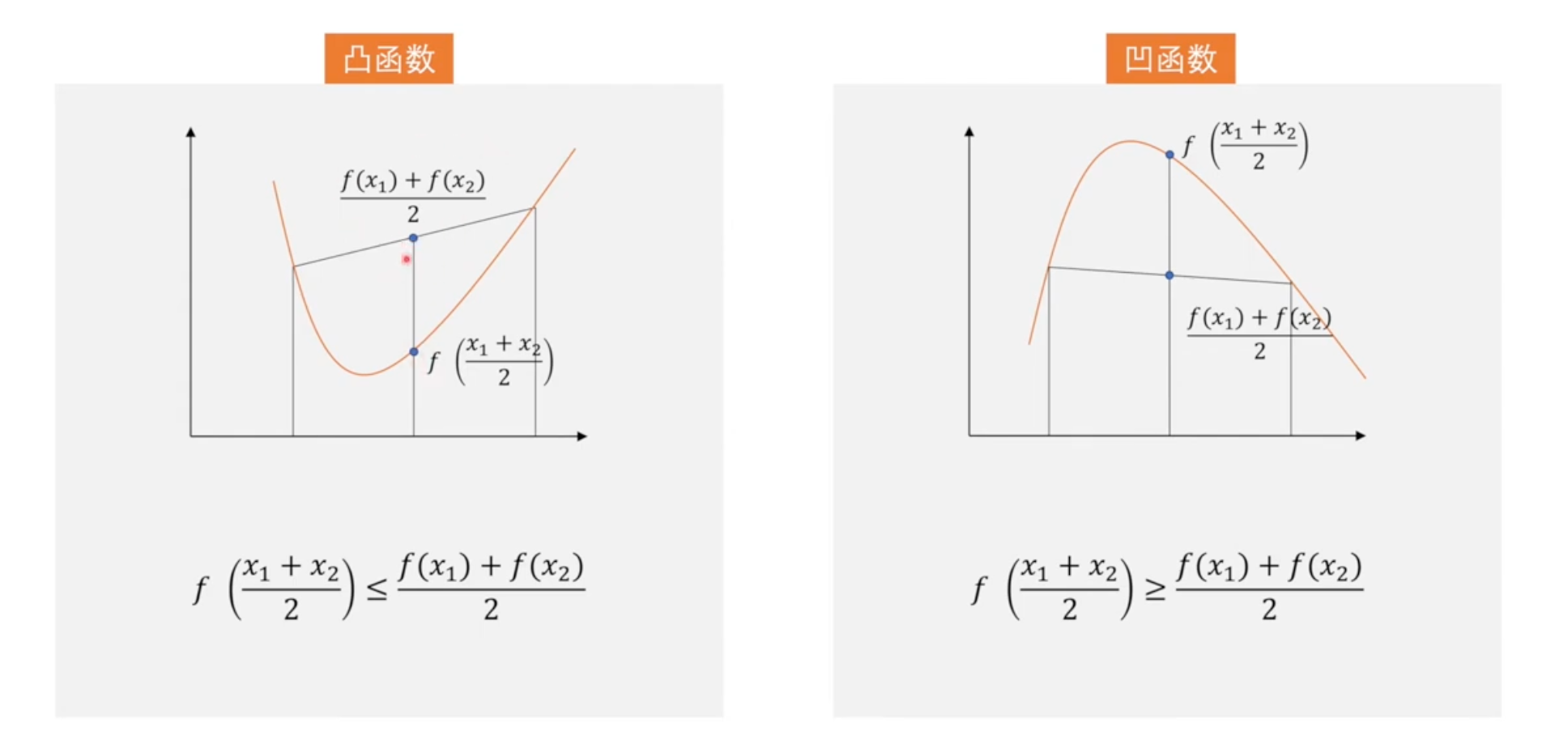
image-20240930214455580

假设说找到一个 x∗=arg⁡min⁡xL(x,λ,μ)x^*=\arg\min_{x} L(x,\lambda,\mu)，则有

g(λ,μ)=f(x∗)+∑λigi(x∗)+∑μihi(x∗)g(\lambda,\mu)=f(x^*)+\sum\lambda_i g_i(x^*)+\sum\mu_i h_i(x^*)

关于 λ\lambda 和 μ\mu 的一阶线性的 gg 函数确定的是一条直线（求最大值：凹函数）

总结

  • 原问题

    min⁡xmax⁡λ,μL(x,λ,μ)s.t. λ≥0\min_{x}\max_{\lambda,\mu} L(x,\lambda,\mu)\\ s.t.\ \lambda\ge0

    这种形式的表达等价于

    min⁡xf(x)s.t. gi(x)≤0,i=1,2,…,mhi(x)=0,i=1,2,…,q\min_x f(x)\\ s.t.\ g_i(x)\le0,i=1,2,\dots,m\\ h_i(x)=0,i=1,2,\dots,q

  • 对偶问题

    max⁡λ,μg(λ,μ)=max⁡λ,μmin⁡xL(x,λ,μ)s.t. λ≥0\max_{\lambda,\mu} g(\lambda,\mu)=\max_{\lambda,\mu}\min_{x} L(x,\lambda,\mu)\\ s.t.\ \lambda\ge0

  • 比较二者

    max⁡λ,μL(x,λ,μ)≥L(x,λ,μ)≥min⁡xL(x,λ,μ)↓A(x)=max⁡λ,μL(x,λ,μ)≥L(x,λ,μ)≥min⁡xL(x,λ,μ)=I(λ,μ)↓A(x)≥I(λ,μ)↓A(x)≥min⁡xA(x)≥max⁡λ,μI(λ,μ)=I(λ,μ)↓P∗=min⁡xA(x)≥max⁡λ,μI(λ,μ)=D∗\max_{\lambda,\mu} L(x,\lambda,\mu)\ge L(x,\lambda,\mu)\ge \min_x L(x,\lambda,\mu)\\ \downarrow\\ A(x)=\max_{\lambda,\mu} L(x,\lambda,\mu)\ge L(x,\lambda,\mu)\ge\min_{x} L(x,\lambda,\mu)=I(\lambda,\mu)\\ \downarrow\\ A(x)\ge I(\lambda,\mu)\\ \downarrow\\ A(x)\ge\min_x A(x)\ge\max_{\lambda,\mu} I(\lambda,\mu)=I(\lambda,\mu)\\ \downarrow\\ P^*=\min_x A(x)\ge\max_{\lambda,\mu} I(\lambda,\mu)= D^*
    • P∗P^* 是原问题的解
    • D∗D^* 是对偶问题的解
min⁡f(x,y)s.t. y=g(x)\min f(x,y)\\ s.t.\ y=g(x) L(x,y,λ)=f(x,y)+λ(y−g(x))↓∇L(x,y,λ)=0↓{∂f(x,y)∂x+λ∂(y−g(x))∂x=0∂f(x,y)∂y+λ∂(y−g(x))∂y=0L(x,y,\lambda)=f(x,y)+\lambda (y-g(x))\\ \downarrow\\ \nabla L(x,y,\lambda)=0\\ \downarrow\\ \begin{cases} \frac{\partial f(x,y)}{\partial x}+\lambda\frac{\partial(y-g(x))}{\partial x}=0\\ \frac{\partial f(x,y)}{\partial y}+\lambda\frac{\partial(y-g(x))}{\partial y}=0 \end{cases}
min⁡f(x),x∈Rns.t. gi(x)=aiT⋅x+bi≤0,i=1,2,…,m,ai∈Rn,bi∈R\min f(x),x\in \mathbb{R}^n\\ s.t.\ g_i(x)=a_i^T\cdot x+b_i\le0,i=1,2,\dots,m,a_i\in\mathbb{R}^n,b_i\in\mathbb{R} L(x,λ)=f(x)+∑i=1mλigi(x)↓∇L(x,λ)=0↓∇f(x)+∑i=1mλi∇gi(x)=0L(x,\lambda)=f(x)+\sum_{i=1}^m\lambda_ig_i(x)\\ \downarrow\\ \nabla L(x,\lambda)=0\\ \downarrow\\ \nabla f(x)+\sum_{i=1}^m\lambda_i \nabla g_i(x)=0

Slater 条件

Slater 条件是强对偶问题的充分条件（只要满足 Slater 条件，就是强对偶；强对偶问题不一定满足 Slater 条件）

Slater 条件的定义：存在一个点 x∈relint Dx\in relint\ D，使得 gi(x)<0g_i(x)\lt0，其中 i=1,2,…,m,Ax=bi=1,2,\dots,m, Ax=b

relint Drelint\ D 表示可行域 DD 的相对内部

如何理解这个鬼定义？

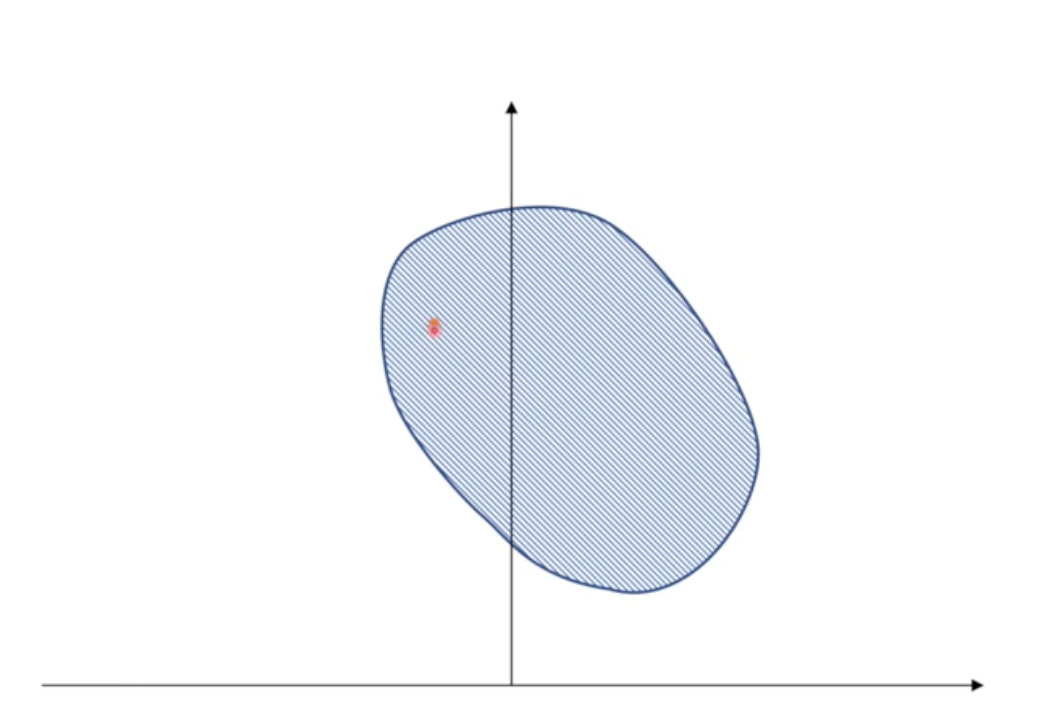
image-20240930231912111

这个定义域的左半边至少存在一个点

KKT 条件

KKT 条件是强对偶问题的必要条件（只要是强对偶问题，一定满足 KKT 条件）

KKT 条件的定义

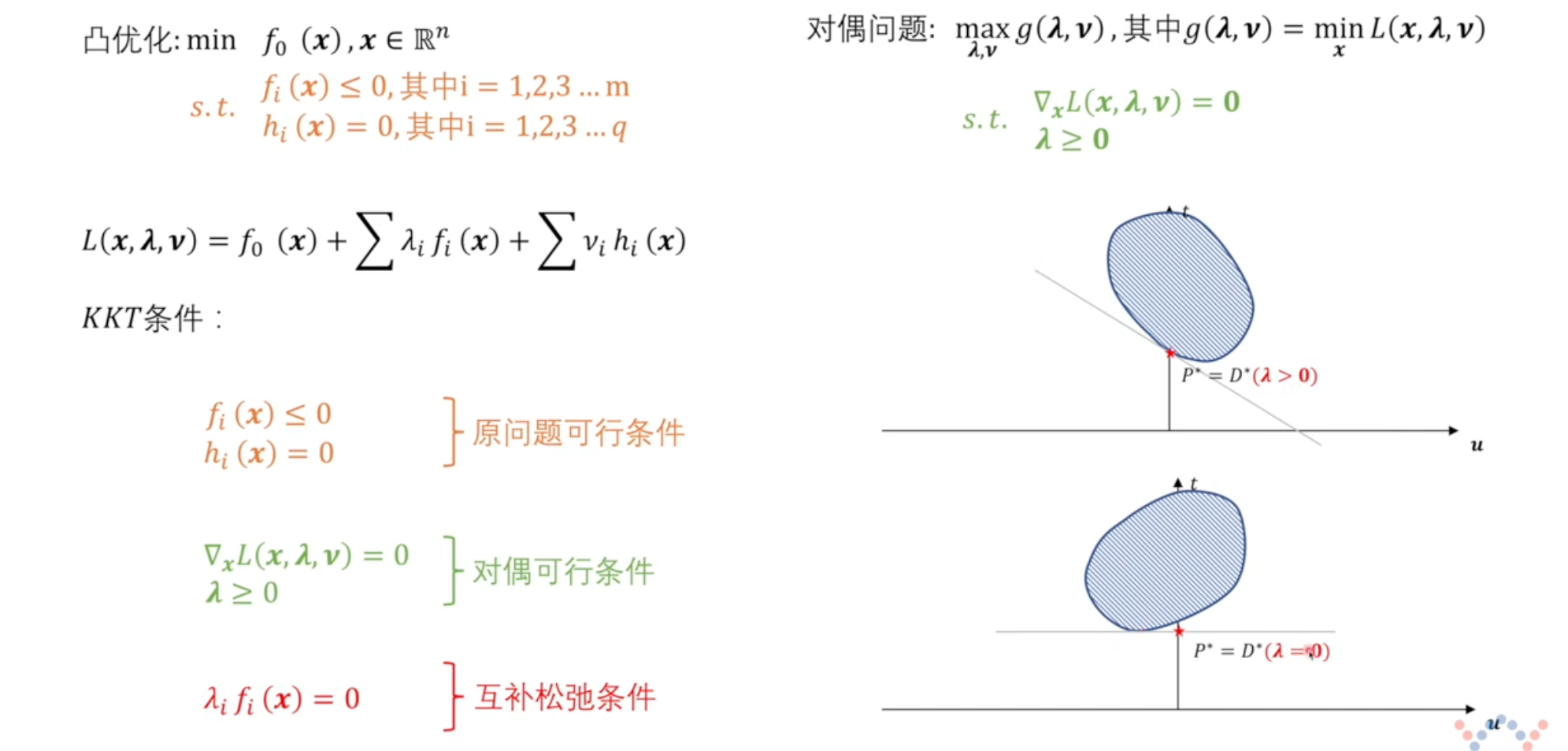
image-20240930232633793

Reference