这学期我学习了三门与数学有关的课程，分别是线性代数、微分方程和选修课探寻数学的理与美。在探寻数学的理与美课上，我从不同老师的讲课中从另一个角度重新审视了数学之美以及它的用途。对于我而言，微分方程的用途总是十分直观的，而与之相比，线性代数则显得更加偏教科书化。尽管我学习了线性代数的各种基本知识与定理，但我仍然对其中的各种概念如特征值、零空间等缺乏立体的审视，因此我在课外阅读了许多将线性代数与几何相结合的资料，对知识的巩固加深了理解。在其中，令我印象最深的就是奇异值分解以及它在压缩图像上的应用。

由于本学期的课程上教授还未教授奇异值分解的内容，对于奇异值分解相关知识的学习我几乎都是从不同的电子书以及一个名为“线代启示录”的台湾博客中了解到。一开始我先是粗略地浏览了很多资料，了解到奇异值分解的目的是为了把一个$m\times n$ 的矩阵分解成一个特定的形式。这种形式有点类似于我已经学习了的正交对角化的知识，只不过它处理的是一个正方形的矩阵，且有一定的局限性。在大多数的资料上，我发现它们都没有直接介绍奇异值分解的形式，而是引入了一个式子的推导：$Av_i=\sigma_iu_i$。其中$A$是一个$m\times n$的矩阵，$\sigma_i$是其所对应的奇异值。

关于这个式子是如何来的，我主要参考了“线代启示录”的作者的思路。值得一提的是，从这个博客里我意外地发现在台湾对矩阵的行与列的定义与我们居然是相反的。台湾文章中的行是我们所指的列，而列是我们所指的行，这点导致了我在阅读相关文章的时候产生了不小的误解，幸而作者标记了英文的 row 与 col 的注释，这大大降低了我阅读时的难度。为了得到$Av_i=\sigma_iu_i$的推导，这个作者分别对两个正方形矩阵$A^TA$和$AA^T$进行了分析。其中先是设$v_i$为$A^TA$的单位正交化的空间，然后证明了其中一部分对应的是原矩阵$A$的行空间，一部分对应的是零空间。接着，作者十分巧妙地利用$Av_i=\sigma_iu_i$的式子设了一组$u_i$，并证明了每一个$v_i$所对应产生的$u_i$也分别对应了原矩阵的列空间和左零空间。从而最终确立了$Av_i=\sigma_iu_i$的存在性。

其中最令我感到神奇的是在处理$u_i$时用到的巧妙地假设。我完全无法体会到前人是如何提出这种设法来的，虽然理解证明的过程非常简单，但是这种感觉有点像是已经站在了巨人的肩膀上看到了世界，知道了结果推出证明的感觉，这让我十分佩服第一个想到这种方法的人。整个证明过程整理如下：

对于矩阵$A^TA_{n\times n}$，假设对于 $A^TA$的特征值和特征向量为: $A^TAv_i=\sigma_i^2v_i,\ i=1,2,\ldots,n$

$$\begin{aligned} A^TA[v_1:v_2:\vdots:v_n]=&[A^TAv_1:A^TAv_2:\dots:A^TAv_n]\\=& [\sigma_1^2v_1:\sigma_2^2v_2:\dots:\sigma_n^2v_n] \\=&[v_1:v_2:\dots:v_n] \left[ \begin{matrix}\sigma_1^2&0&\cdots&0 \\ 0&\sigma_2^2&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&\sigma_n^2\end{matrix} \right] \end{aligned}$$

令矩阵$V$ 为$[v_1:v_2:\dots:v_n]$

$$A^TA=V\left[ \begin{matrix} \sigma_1^2&0&\cdots&0 \\ 0&\sigma_2^2&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&\sigma_n^2\end{matrix} \right]V^{-1}=V\left[ \begin{matrix} \sigma_1^2&0&\cdots&0 \\ 0&\sigma_2^2&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&\sigma_n^2\end{matrix} \right]V^{T}$$

假设 $rank(A^TA)=rank(\begin{bmatrix} \sigma_1^2&0&\cdots&0 \\ 0&\sigma_2^2&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&\sigma_n^2\end{bmatrix})=r$

让 $\sigma_1\ge\sigma_2\ge\dots\ge\sigma_r\gt0,\ \sigma_{r+1}=\sigma_{r+2}=\dots=\sigma_n=0$

$$\because\ A^TAv_i=\sigma_i^2v_i\\$$ $$\therefore\ v_i^TA^TAv_i=v_i^T\sigma_i^2v_i=\sigma_i^2\\ \| Av_i \|^2=\sigma_i^2$$ $$\because\ \sigma_i=0,\ i=r+1,r+2,\dots,n \\$$ $$\therefore\ Av_i=0,\ i=r+1,r+2,\dots,n\\\Rightarrow null(A)=span(v_{r+1},v_{r+2},\ldots,v_n)=row(A)^{\perp}$$ $$\because\ span(v_1,v_2,\ldots,v_r)\perp span(v_{r+1},v_{r+2},\ldots,v_n)=row(A)^\perp\\$$ $$\Rightarrow \ row(A)=span(v_1,v_2,\ldots,v_r)$$

接着对$AA^T_{m\times m}$进行操作

假设对于 $AA^T_{m\times m}$ 有向量 $u_i=\frac{Av_i}{\sigma_i}, i=1,2,\ldots,r$

$$\begin{aligned}u_i\cdot u_y=u_i^Tu_y = &\frac{(Av_i)^T}{\sigma_i}\frac{Av_j}{\sigma_j} \\=& \frac{v_i^TA^T}{\sigma_i}\frac{Av_j}{\sigma_j}=\frac{v_i^T(A^TAv_j)}{\sigma_i\sigma_j}\\=&\frac{v_i^T(\sigma_j^2v_j)}{\sigma_i\sigma_j}=\frac{\sigma_j^2}{\sigma_i\sigma_j}v_i^Tv_j \\=&\left\{\begin{aligned} &0,&for\ i\ne j\\&1,&for\ i=j\end{aligned} \right.\end{aligned}$$ $$row(A^T)=col(A)=span(u_1,u_2,\ldots,u_r)\\null(A^T)=span(u_{r+1},u_{r+2},\ldots,u_m)$$

也由此，我明白了在奇异值分解中每个符号所代表的意义。重新审视$Av_i=\sigma_iu_i$这个式子，$\sigma$仿佛是一个有魔力的戒指，将一个矩阵的行空间、列空间、零空间和左零空间都紧紧联系在了一起，而奇异值分解的标准形式，只不过将 A 的各个空间构建成了新的矩阵形式，最后再利用对角矩阵的特殊性质分解成了一项一项的形式，分解过程如下：

假设矩阵 $A_{m\times n}$, $rank(A )=r$, 它的奇异值分解为 $A=U\Sigma V^T$

$$U_{m\times m}=[u_1:u_2:\ldots:u_m]$$ $$\Sigma_{m\times n}=\begin{bmatrix} \sigma_{1} & 0 & 0 & 0 &\cdots &0\\ 0 & \ddots & 0 & \vdots & \cdots & 0\\ 0 & 0 & \sigma_{r} & 0 &\cdots & 0\\ 0 & \cdots & 0 & 0 & \cdots &0\\ \vdots&\ddots&\vdots&\vdots&\ddots&\vdots\\0 & \cdots & 0 & 0 & \cdots & 0 \end{bmatrix}$$ $$V_{n\times n}=[v_1:v_2:\ldots:v_n]$$ $$\begin{aligned}A=&[u_1:u_2:\ldots:u_m]\begin{bmatrix} \sigma_{1} & 0 & 0 & 0 &\cdots &0\\ 0 & \ddots & 0 & \vdots & \cdots & 0\\ 0 & 0 & \sigma_{r} & 0 &\cdots & 0\\ 0 & \cdots & 0 & 0 & \cdots &0\\ \vdots&\ddots&\vdots&\vdots&\ddots&\vdots\\0 & \cdots & 0 & 0 & \cdots & 0 \end{bmatrix}\begin{bmatrix}v_1^T\\v_2^T\\\vdots \\v_n^T\end{bmatrix}\\=&[\sigma_1u_1:\sigma_2u_2:\ldots:\sigma_ru_r:0:\ldots:0]\begin{bmatrix}v_1^T\\v_2^T\\\vdots \\v_n^T\end{bmatrix}\\=&\sum_{i=1}^r\sigma_iu_iv_i^T\end{aligned}$$

学到了这个地方，我已经对奇异值分解具有初步的了解了。在浏览不同教材与网站的过程中，我的余光总是看到“图片压缩”这个词。一开始我并想不到这个式子能和压缩产生什么关系，但是反复盯着奇异值分解的标准形式$A=\sum_{i=1}^r\sigma_iu_iv_i^T$后，我猛地意识到这个式子不就是很多项一个常数乘上一个矩阵再相加每一项的形式吗。其中每一个常数就是这个矩阵的一项项奇异值，由于每项的矩阵行与列的大小都是一样的，每一个矩阵都在形成矩阵$A$中占有一定的权重，而这个权重就是该项对应的奇异值的大小。倘若这个奇异值十分小，那么即使抛弃了这一项的矩阵所形成的矩阵$A$也不会与正确的矩阵$A$相差太多。这个抛弃的过程不就是压缩吗？为了验证我的猜想，我查阅了相关的资料，最后发现我的想法是十分正确的。为了验证我的想法，我打算亲自利用奇异值分解压缩一张图片试试。

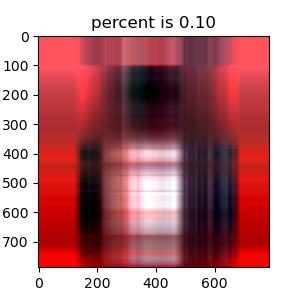
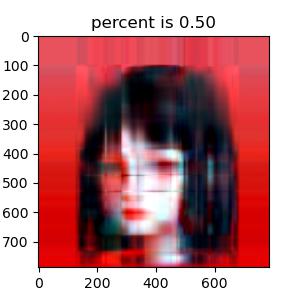
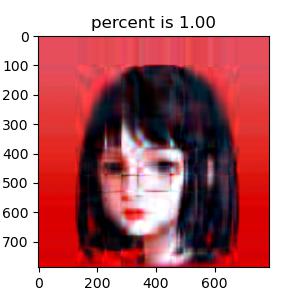
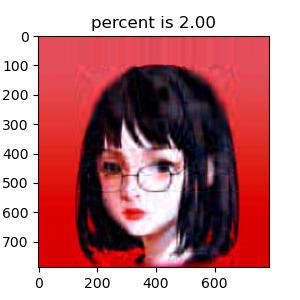
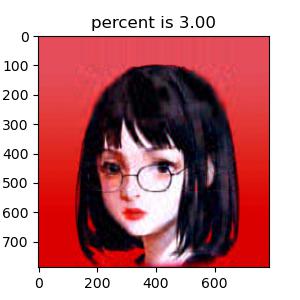
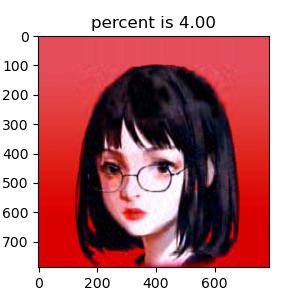
我选择了我的头像（如图）作为试验的对象，并使用了两个 Python 环境中的开源模块 Numpy 和 Matplotlib 来计算奇异值分解与读取图片。首先我便遇到了读取图片的困难。由于图片是彩色的，其导入到计算机的矩阵并不是一个二维矩阵，而是类似与$(m,n,3)$的三维数组。其中 3 代表了图片的 rgb 三个颜色通道，每一个位置对应了一个 0-255 间的颜色数值。我先想到的是有没有什么办法对一个高维数组进行奇异值分解，但并不能找到答案。接着我从 Numpy 的一个栈相关的函数中得到了启发，意识到可以将三个颜色通道进行分别处理，这样就可以得到 3 个二维矩阵的奇异值分解，最后再把它们加起来即可。代码如下：

import numpy as np
import matplotlib.pyplot as plt

sample = plt.imread("sample.jpg")
sample = np.array(sample)
m, n = sample[:, :, 0].shape

r = sample[:, :, 0]
g = sample[:, :, 1]
b = sample[:, :, 2]
fig, ax = plt.subplots(1, 3)
ax[0].imshow(r)
ax[0].set_title('R channel')
ax[1].imshow(g)
ax[1].set_title('G channel')
ax[2].imshow(b)
ax[2].set_title('B channel')
plt.show()

def SVD_compression(channel, p):
    U, sig, V_T = np.linalg.svd(channel)
    newChannel = np.zeros((m, n))
    for i in range(len(sig)):
        newChannel += sig[i] * (U[:, i].reshape(m, 1)@V_T[i, :].reshape(1, n))
        if float(i) / len(sig) > p:
            newChannel[newChannel < 0] = 0
            newChannel[newChannel > 255] = 255
            break
    return newChannel.astype('i2')

说到最重要的奇异值分解部分，不得不感谢 Numpy 模块 linalg 下自带的 svd 函数，使我省去了最繁琐的过程。为了清晰对比出我保留不同数量$\sigma$对图片压缩的影响，我定义了一个 p 值用来表示保留的$\sigma$个数占非零$\sigma$总个数的占比，最后得到的压缩代码与结果如下。事实证明，奇异值分解对于压缩图片取得的效果是十分显著的，即使我取一个很少很少数量也就是很小很小的 p 值，图片也能压缩得与原图差不多清晰。这个压缩过程令我大为震撼，感叹于小小的公式在这个复杂的过程中发挥出的巨大的作用，也联想到不光是图片，或许是一切可以想法设法表现成矩阵的信息，如音频都可以通过奇异值分解的方式进行压缩。那么奇异值虽然是奇异值，那它到底是什么呢？它附着信息的神奇深深地吸引到我了，让我对线代这门学科产生了更多的好奇与思考。